Entropy
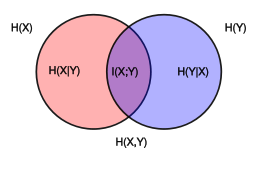 Today I was trying to see the relationships between information, entropy, cross entropy, conditional entropy, the Kullback-Leibler divergence and all that fuzz.
Today I was trying to see the relationships between information, entropy, cross entropy, conditional entropy, the Kullback-Leibler divergence and all that fuzz.
As a quick reminder:
- Information content (of a random variable): $I(X) = – \log(P(X))$
- Entropy (of a random variable): $H(X) = E[I(X)] = E[– \log(P(X))]$
- Conditional Entropy (of a random variable on another): $H(X|Y) = E{PY}[H(X|Y=y)]$
- Cross Entropy (between two probability distributions): $H(p, q) = Ep[– \log q] = H(p) + D{KL}(p | q)$
- Kullback-Leibler divergence (from probability distribution $q$ to $p$): $D_{KL}(p | q) = H(p, q) – H(p)$
The Kullback-Leibler divergence is surprisingly useful in many places. For example, it can be something to maximize (its expected value), as a criterion for experimental design. I wish I had known more about it during the time of writing my thesis.
I wish I'd write about the interpretation of $D_{KL}$ as a measure of the information gained when one changes from using the probability distribution $q$ to $p$. But if I do, I'll never click the “Publish” button :)